Berikut ini adalah penjelasan lengkap tentang algoritma Kruskal, sebuah algoritma yang digunakan untuk menyelesaikan masalah pohon minimal dalam graf. Algoritma ini sangat berguna dalam berbagai bidang seperti jaringan komputer, optimasi rute, dan masih banyak lagi.
Soal 1: Apa itu algoritma Kruskal?
Algoritma Kruskal adalah algoritma yang digunakan untuk menyelesaikan masalah pohon minimal dalam graf. Algoritma ini mencari pohon minimal dengan memilih tepi dengan bobot terkecil secara berurutan dari graf yang belum terhubung.
Soal 2: Apa manfaat dari algoritma Kruskal?
Algoritma Kruskal sangat berguna dalam berbagai bidang seperti jaringan komputer, optimasi rute, dan masih banyak lagi. Dengan algoritma Kruskal, kita dapat menyelesaikan masalah pohon minimal dengan cepat dan mudah.
Soal 3: Apa langkah-langkah dalam algoritma Kruskal?
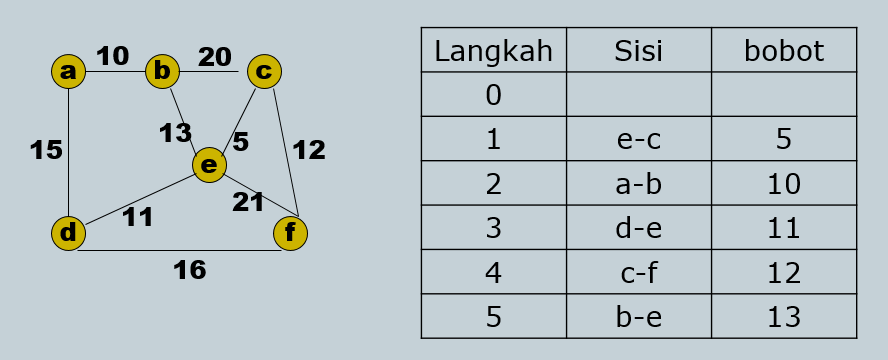
Berikut adalah langkah-langkah dalam algoritma Kruskal:
- Urutkan semua tepi dalam graf berdasarkan bobotnya dari yang terkecil hingga terbesar.
- Pilih tepi dengan bobot terkecil dan periksa apakah menghubungkan dua pohon yang berbeda.
- Jika ya, tambahkan tepi tersebut ke pohon minimal dan gabungkan kedua pohon.
- Ulangi langkah 2-3 hingga semua titik dalam graf terhubung.
Soal 4: Apa contoh penggunaan algoritma Kruskal?
Contoh penggunaan algoritma Kruskal adalah dalam penyelesaian masalah jaringan komputer. Dalam jaringan komputer, kita ingin mencari rute terpendek antara dua titik. Algoritma Kruskal dapat membantu kita menemukan rute terpendek dengan memilih jalur dengan bobot terkecil secara berurutan.
Soal 5: Apa perbedaan antara algoritma Kruskal dan algoritma Prim?
Perbedaan antara algoritma Kruskal dan algoritma Prim adalah bahwa algoritma Kruskal memilih tepi dengan bobot terkecil secara berurutan, sedangkan algoritma Prim memilih titik dengan jarak terdekat dari pohon minimal saat ini.
Soal 6: Apa keuntungan dari algoritma Kruskal?
Keuntungan dari algoritma Kruskal adalah bahwa algoritma ini mudah dipahami dan diimplementasikan. Selain itu, algoritma Kruskal memiliki kompleksitas waktu yang cukup cepat, yaitu O(E log E), di mana E adalah jumlah tepi dalam graf.
Soal 7: Apa kompleksitas waktu algoritma Kruskal?
Kompleksitas waktu algoritma Kruskal adalah O(E log E), di mana E adalah jumlah tepi dalam graf.
Soal 8: Apa kelemahan dari algoritma Kruskal?
Kelemahan dari algoritma Kruskal adalah bahwa algoritma ini tidak efisien untuk graf yang sangat besar. Selain itu, algoritma Kruskal tidak dapat menyelesaikan masalah graf yang mengandung sirkuit.
Soal 9: Bagaimana cara mengimplementasikan algoritma Kruskal dalam bahasa pemrograman?
Untuk mengimplementasikan algoritma Kruskal dalam bahasa pemrograman, kita perlu mengurutkan semua tepi dalam graf berdasarkan bobotnya, lalu memilih tepi dengan bobot terkecil dan memeriksa apakah menghubungkan dua pohon yang berbeda. Jika ya, tambahkan tepi tersebut ke pohon minimal dan gabungkan kedua pohon. Ulangi langkah ini hingga semua titik dalam graf terhubung.
Soal 10: Apa kesimpulan dari penjelasan tentang algoritma Kruskal?
Kesimpulan dari penjelasan tentang algoritma Kruskal adalah bahwa algoritma ini sangat berguna dalam menyelesaikan masalah pohon minimal dalam graf. Algoritma Kruskal mudah dipahami dan diimplementasikan, namun tidak efisien untuk graf yang sangat besar dan tidak dapat menyelesaikan masalah graf yang mengandung sirkuit.
Kata Penutup
Algoritma Kruskal adalah algoritma yang sangat berguna dalam berbagai bidang seperti jaringan komputer, optimasi rute, dan masih banyak lagi. Dengan algoritma Kruskal, kita dapat menyelesaikan masalah pohon minimal dengan cepat dan mudah.








Leave a Comment