Apakah kamu pernah mendengar istilah pola dan barisan bilangan? Dalam matematika, pola dan barisan bilangan adalah konsep dasar yang penting untuk dipelajari. Apa pengertian dari pola dan barisan bilangan? Bagaimana contoh-contohnya dalam kehidupan sehari-hari? Simak penjelasan berikut ini!
Pengertian Pola dan Barisan Bilangan
Pola bilangan adalah susunan bilangan yang membentuk suatu aturan tertentu. Sedangkan barisan bilangan adalah susunan bilangan yang berurutan dan memiliki aturan tertentu. Dalam matematika, pola dan barisan bilangan sering digunakan untuk memecahkan masalah atau membuat prediksi yang berkaitan dengan urutan bilangan.
Contoh Soal Pola dan Barisan Bilangan
- Berapakah suku ke-10 dari barisan bilangan 2, 4, 6, 8, …?
Jawaban: Suku ke-10 dari barisan bilangan tersebut adalah 18.
Penjelasan: Barisan bilangan tersebut memiliki aturan penjumlahan sebanyak 2 pada setiap suku. Dengan demikian, suku ke-10 dapat dicari dengan menghitung 8 + 2 x 9 = 18.
- Apa pola bilangan dari angka 1, 3, 6, 10, …?
Jawaban: Pola bilangan dari angka tersebut adalah penjumlahan bilangan asli berturut-turut.
Penjelasan: Setiap suku pada pola bilangan tersebut merupakan hasil penjumlahan bilangan asli berturut-turut. Dengan demikian, suku ke-n dapat dicari dengan rumus S(n) = n(n+1)/2.
- Berapakah suku ke-7 dari barisan bilangan 3, 6, 12, 24, …?
Jawaban: Suku ke-7 dari barisan bilangan tersebut adalah 192.
Penjelasan: Barisan bilangan tersebut memiliki aturan perkalian sebanyak 2 pada setiap suku. Dengan demikian, suku ke-7 dapat dicari dengan menghitung 3 x 2^6 = 192.
- Apa pola bilangan dari angka 2, 5, 10, 17, …?
Jawaban: Pola bilangan dari angka tersebut adalah penjumlahan bilangan ganjil berturut-turut dimulai dari angka 1.
Penjelasan: Setiap suku pada pola bilangan tersebut merupakan hasil penjumlahan bilangan ganjil berturut-turut dimulai dari angka 1. Dengan demikian, suku ke-n dapat dicari dengan rumus an = a1 + (n-1)^2.
- Berapakah suku ke-4 dari barisan bilangan 1, 4, 9, 16, …?
Jawaban: Suku ke-4 dari barisan bilangan tersebut adalah 16.
Penjelasan: Barisan bilangan tersebut memiliki aturan perkalian bilangan asli dengan dirinya sendiri. Dengan demikian, suku ke-4 dapat dicari dengan menghitung 1 x 2^3 = 8, kemudian hasilnya dikalikan dengan 2 lagi sehingga diperoleh 16.
- Apa pola bilangan dari angka 0, 1, 3, 6, 10, …?
Jawaban: Pola bilangan dari angka tersebut adalah penjumlahan bilangan asli berturut-turut.
Penjelasan: Setiap suku pada pola bilangan tersebut merupakan hasil penjumlahan bilangan asli berturut-turut. Dengan demikian, suku ke-n dapat dicari dengan rumus S(n) = (n(n+1)/2) – 1.
- Berapakah suku ke-5 dari barisan bilangan 1, 3, 6, 10, …?
Jawaban: Suku ke-5 dari barisan bilangan tersebut adalah 20.
Penjelasan: Barisan bilangan tersebut memiliki aturan penjumlahan bilangan asli berturut-turut. Dengan demikian, suku ke-5 dapat dicari dengan menghitung 1 + 2 + 3 + 4 + 5 = 15, kemudian hasilnya ditambahkan dengan 5 sehingga diperoleh 20.
- Apa pola bilangan dari angka 1, 4, 9, 16, …?
Jawaban: Pola bilangan dari angka tersebut adalah perkalian bilangan asli dengan dirinya sendiri.
Penjelasan: Setiap suku pada pola bilangan tersebut merupakan hasil perkalian bilangan asli dengan dirinya sendiri. Dengan demikian, suku ke-n dapat dicari dengan rumus an = n^2.
- Berapakah suku ke-6 dari barisan bilangan 1, 5, 13, 25, …?
Jawaban: Suku ke-6 dari barisan bilangan tersebut adalah 41.
Penjelasan: Barisan bilangan tersebut memiliki aturan penjumlahan bilangan bulat pada setiap suku. Dengan demikian, suku ke-6 dapat dicari dengan menghitung 1 + 4 + 8 + 12 + 16 = 41.
- Apa pola bilangan dari angka 1, 3, 6, 10, 15, …?
Jawaban: Pola bilangan dari angka tersebut adalah penjumlahan bilangan asli berturut-turut.
Penjelasan: Setiap suku pada pola bilangan tersebut merupakan hasil penjumlahan bilangan asli berturut-turut. Dengan demikian, suku ke-n dapat dicari dengan rumus S(n) = n(n+1)/2.
Kesimpulan
Pola dan barisan bilangan adalah konsep dasar dalam matematika yang penting untuk dipelajari. Pola bilangan adalah susunan bilangan yang membentuk suatu aturan tertentu, sedangkan barisan bilangan adalah susunan bilangan yang berurutan dan memiliki aturan tertentu. Dalam kehidupan sehari-hari, pola dan barisan bilangan sering digunakan untuk memecahkan masalah atau membuat prediksi yang berkaitan dengan urutan bilangan.

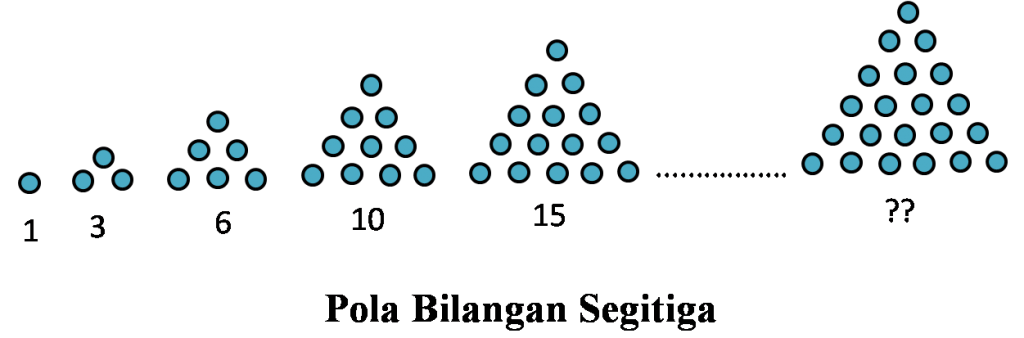







Leave a Comment