Hyperbola adalah salah satu bentuk kurva yang ditemukan dalam matematika. Kurva ini memiliki sifat yang unik dan sering digunakan dalam berbagai bidang, seperti fisika, astronomi, dan teknik. Dalam artikel ini, kita akan membahas tentang pengertian dan contoh dari hyperbola beserta dengan beberapa soal dan jawaban untuk membantu memahami materi lebih dalam.
Pengertian Hyperbola
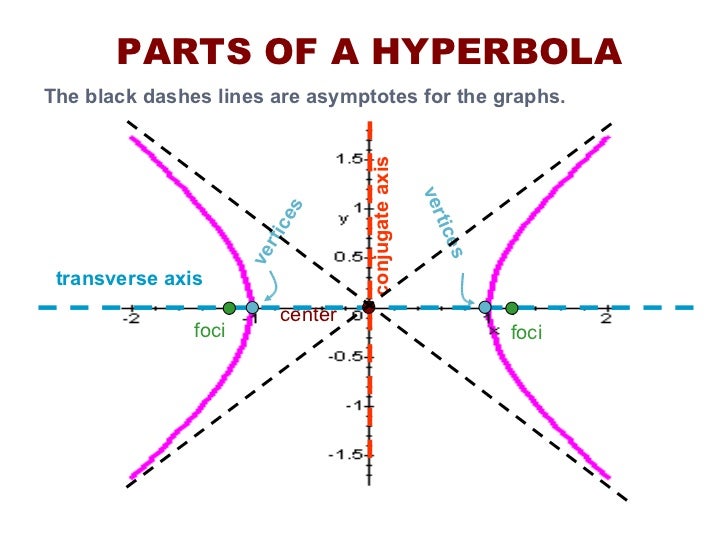
Hyperbola adalah kurva yang dibentuk oleh semua titik-titik (x,y) dalam koordinat kartesius yang memiliki perbedaan jarak yang konstan dari dua titik tetap yang disebut fokus dan terletak pada sumbu utama kurva. Perbedaan jarak ini disebut konstanta pemusatan atau disebut juga sebagai jarak fokus.
Contoh Hyperbola
Salah satu contoh paling umum dari hyperbola adalah orbit planet dan satelit di sekitar Matahari. Orbit ini membentuk kurva hyperbola karena planet dan satelit bergerak dengan kecepatan yang berbeda-beda sepanjang orbitnya dan selalu berada pada jarak yang sama dari Matahari.
Contoh lain dari hyperbola adalah pada kabel telegraf bawah laut. Kabel ini memiliki bentuk hyperbola karena jarak dari kedua ujung kabel tetap sama dan sinyal yang dikirimkan melalui kabel bergerak dengan kecepatan yang berbeda-beda.
Soal dan Jawaban
- Apa yang dimaksud dengan hyperbola?
- Apa yang dimaksud dengan konstanta pemusatan pada hyperbola?
- Apa yang menjadi contoh paling umum dari hyperbola?
- Apa yang menjadi contoh lain dari hyperbola?
- Bagaimana cara menentukan fokus pada hyperbola?
- Carilah jarak antara kedua titik tetap yang diberikan dan bagi hasilnya dengan dua.
- Pindahkan titik pusat kurva ke titik tengah antara dua titik tetap.
- Tentukan arah sumbu utama hyperbola berdasarkan sudut yang dibentuk oleh garis yang menghubungkan dua titik tetap dan sumbu x.
- Tentukan jarak antara pusat kurva dan salah satu titik tetap, inilah jarak fokus.
- Bagaimana cara menentukan sumbu utama pada hyperbola?
- Apa yang dimaksud dengan asimtot pada hyperbola?
- Bagaimana cara menentukan persamaan umum hyperbola?
- Apa yang dimaksud dengan eksentrisitas pada hyperbola?
- Bagaimana cara menentukan titik potong sumbu pada hyperbola?
Hyperbola adalah kurva yang dibentuk oleh semua titik-titik (x,y) dalam koordinat kartesius yang memiliki perbedaan jarak yang konstan dari dua titik tetap yang disebut fokus dan terletak pada sumbu utama kurva.
Perbedaan jarak antara dua titik tetap yang disebut fokus pada hyperbola disebut konstanta pemusatan atau jarak fokus.
Orbit planet dan satelit di sekitar Matahari merupakan contoh paling umum dari hyperbola.
Kabel telegraf bawah laut merupakan contoh lain dari hyperbola.
Sumbu utama pada hyperbola dapat ditentukan dengan menggunakan sudut yang dibentuk oleh garis yang menghubungkan titik-titik tetap dan sumbu x. Sumbu utama akan selalu tegak lurus dengan garis yang menghubungkan dua titik tetap.
Asimtot pada hyperbola adalah dua garis yang mendekati kurva hyperbola namun tidak pernah memotongnya. Garis ini selalu memiliki sudut tertentu terhadap sumbu utama pada hyperbola.
Persamaan umum hyperbola adalah (x-h)^2/a^2 – (y-k)^2/b^2 = 1 atau (y-k)^2/b^2 – (x-h)^2/a^2 = 1
Eksentrisitas pada hyperbola adalah rasio antara jarak fokus dan jarak dari titik pusat ke salah satu titik potong sumbu utama. Eksentrisitas selalu lebih besar dari 1 dan semakin besar eksentrisitas maka semakin meruncing kurva hyperbola.
Titik potong sumbu pada hyperbola dapat ditentukan dengan mengganti salah satu variabel menjadi 0 pada persamaan umum hyperbola. Jika variabel x diganti menjadi 0, maka kita akan mendapatkan titik potong sumbu y, begitu juga sebaliknya.
Kesimpulan
Hyperbola adalah salah satu bentuk kurva yang unik dan sering digunakan dalam berbagai bidang. Kurva ini memiliki sifat yang unik dan dapat digunakan untuk memodelkan banyak fenomena alam dan teknik. Dengan memahami konsep dan sifat-sifat dasar dari hyperbola, kita dapat memahami lebih dalam tentang bagaimana bentuk kurva ini dapat digunakan dalam berbagai bidang.







Leave a Comment